Координатна пряма. Точки на координатної прямої. Як побудувати координатну пряму

Стверджувати, що ви знаєте математику, неможливо,якщо ви не вмієте будувати графіки, зображати нерівності на координатної прямої, працювати з осями координат. Візуальна складова в науці життєво необхідна, адже без наочних прикладів в формулах і обчисленнях часом можна сильно заплутатися. У даній статті ми подивимося, як працювати з осями координат, і навчимося будувати найпростіші графіки функцій.

застосування

Координатна пряма - це основа найпростіших видівграфіків, з якими стикається школяр на своєму навчальному шляху. Вона використовується практично в кожній математичної темі: при розрахунку швидкості і часу, проектуванні розмірів об'єктів і обчисленні їх площі, в тригонометрії при роботі з синусами і косинусами.

Головна цінність такої прямої - це наочність. Оскільки математика - це наука, в якій потрібен високий рівень абстрактності мислення, графіки допомагають в поданні об'єкта в реальному світі. Як він себе веде? В якій точці простору буде перебувати через кілька секунд, хвилин, годин? Що можна сказати про нього в зіставленні з іншими об'єктами? Якою швидкістю він має в випадково обраний момент часу? Як охарактеризувати його рух?

А про швидкість мова йде не просто так - саме їїчасто відображають графіки функції. А ще вони можуть відображати зміна температури або тиску всередині об'єкта, його розмірів, орієнтації відносно горизонту. Таким чином, побудувати координатну пряму найчастіше потрібна і в фізиці.

Одновимірна графік

Існує поняття багатовимірності. В одновимірному просторі достатньо всього одного числа, щоб визначити місце розташування точки. Це як раз і є випадок із застосуванням координатної прямої. Якщо простір двомірне, то буде потрібно два числа. Графіки такого типу використовуються набагато частіше, і трохи далі в статті ми їх обов'язково розглянемо.

Що можна побачити за допомогою точок на осі, якщовона всього одна? Можна побачити розмір об'єкта, його положення в просторі щодо деякого «нуля», т. Е. Точки, обраної в якості початку відліку.

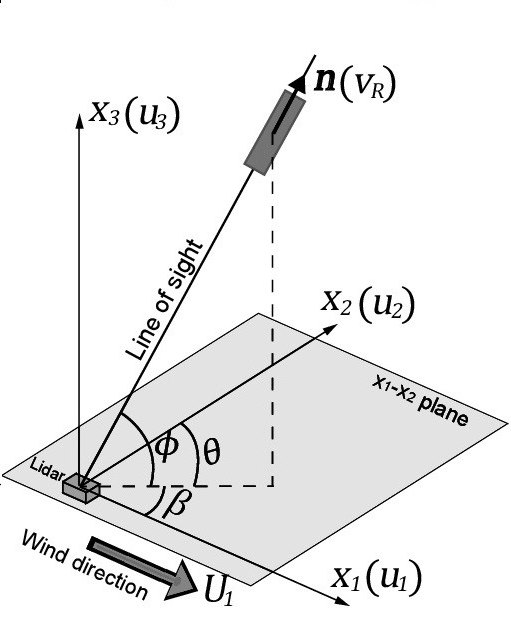
Зміна параметрів з плином часу побачити не вдасться, так як всі свідчення будуть відображатися для одного конкретного моменту. Однак з чогось треба починати! Отже, приступимо.

Як побудувати координатну вісь

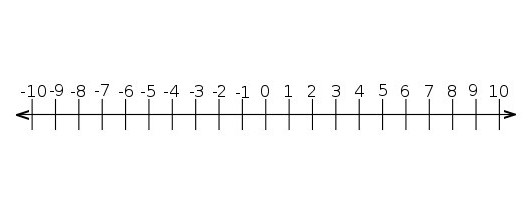
Для початку потрібно провести горизонтальнулінію - це і буде наша вісь. З правого боку «загострити» її, щоб вона була схожа на стрілку. Таким чином ми позначимо напрямок, в якому числа будуть збільшуватися. У бік зменшення стрілка зазвичай не ставиться. Традиційно вісь спрямована вправо, тому ми просто підемо цим правилом.

Поставимо нульову позначку, яка будевідображати початок координат. Це те саме місце, від якого ведеться відлік, будь то розмір, вага, швидкість або що завгодно інше. Крім нуля, ми обов'язково повинні позначити так звану ціну поділки, т. Е. Ввести стандарт одиниці, відповідно до якої будемо відкладати на осі ті чи інші величини. Це обов'язково потрібно робити, щоб вміти знаходити довжину відрізка на координатній прямій.

Через рівну відстань один від одного поставимоточки або «карби» на лінії, а під ними напишемо відповідно 1,2,3 і так далі. І ось, все готово. Але з отриманим графіком треба ще навчитися працювати.

Види точок на координатній прямій

З першого погляду на запропоновані в підручникахмалюнки стає зрозуміло: точки на осі можуть бути зафарбовані або НЕ зафарбовані. Ви думаєте, це випадковість? Зовсім ні! «Суцільна» точка використовується при нестрогому нерівності - тому, яке читається як «більше або дорівнює». Якщо ж потрібно строго обмежити інтервал (наприклад, «ікс» може приймати значення від нуля до одиниці, але не включає її), ми скористаємося «порожнистої» точкою, тобто, по суті, маленьким кружком на осі. Треба зауважити, що учні не дуже люблять строгі нерівності, тому що з ними складніше працювати.

Залежно від того, які точки ви використовуєтена графіку, будуть називатися і побудовані інтервали. Якщо нерівність з двох сторін Нечитка, то ми отримаємо відрізок. Якщо з одного боку він виявиться «відкритий», то називатися буде напівінтервалів. Нарешті, якщо частина прямої обмежена з двох сторін порожніми точками, вона буде називатися інтервалом.

площина

При побудові двох прямих на координатноїплощині ми вже можемо розглядати графіки функцій. Скажімо, горизонтальна лінія буде віссю часу, а вертикальна - відстанню. І ось уже ми в змозі визначити, яку відстань подолає об'єкт через хвилину або годину шляху. Таким чином, робота з площиною дає можливість стежити за зміною стану об'єкта. Це набагато цікавіше, ніж дослідження статичного стану.

Найпростіший графік на такій площині - пряма, вона відображає функцію Y (X) = aX + b. Лінія вигинається? Це означає, що об'єкт змінює свої характеристики в процесі дослідження.

Уявіть, ви стоїте на даху будівлі і тримайтев витягнутій руці камінь. Коли ви відпустите його, він полетить вниз, почавши свій рух з нульовою швидкості. Але вже через секунду він буде долати 36 кілометрів на годину. Камінь продовжить прискорюватися і далі, і щоб намалювати його рух на графіку, вам буде потрібно заміряти його швидкість в кілька моментів часу, виставивши точки на осі у відповідних місцях.

Відмітки на горизонтальній координатній прямій позамовчуванням отримують назву X1, X2, X3, а на вертикальній - Y1, Y2, Y3 відповідно. Проектуючи їх на площину і знаходячи перетину, ми знаходимо фрагменти результуючого малюнка. Поєднавши їх однією лінією, ми отримаємо графік функції. У випадку з падаючим каменем квадратична функція буде мати вигляд: Y (X) = aX * X + bX + c.

масштаб

Звичайно, не обов'язково виставляти поруч зподілами на прямий цілочисельні значення. Якщо ви розглядаєте рух равлики, яка повзе зі швидкістю 0,03 метра в хвилину, виставте в якості значень на координатної прямої дробу. В даному випадку задайте ціну поділки як 0,01 метра.

Особливо зручно виконувати такі креслення в зошитів клітку - тут відразу видно, чи вистачить місця на аркуші для вашого графіка, поки вийдете ви за поля. Свої сили розрахувати нескладно, адже ширина клітини в такий зошити - 0,5 сантиметра. Знадобилося - зменшили малюнок. Від зміни масштабу графіка він не втратить і не змінить своїх властивостей.

Координати точки і відрізка

Коли на уроці дається математична задача, вній можуть міститися параметри різних геометричних фігур як у вигляді довжин сторін, периметра, площі, так і у вигляді координат. У цьому випадку може знадобитися як побудувати фігуру, так і отримати якісь дані, пов'язані з нею. Виникає питання: як знайти на координатної прямої необхідну інформацію? І як побудувати фігуру?

Наприклад, мова йде про точку. Тоді в умові завдання буде фігурувати заголовна буква, а в дужках будуть стояти кілька цифр, частіше всього дві (це означає, вважати ми будемо в двомірному просторі). Якщо в дужках три числа, записані через крапку з комою або через кому, то це тривимірний простір. Кожне із значень - це координата на відповідній осі: спочатку по горизонтальній (X), потім - по вертикальній (Y).

Пам'ятайте, як побудувати відрізок? Ви проходили це на геометрії. Якщо є дві точки, то між ними можна провести пряму. Їх-то координати і вказуються в дужках, якщо в завданні фігурує відрізок. Наприклад: A (15, 13) - B (1, 4). Щоб побудувати таку пряму, потрібно на координатної площині знайти і відзначити точки, а потім їх з'єднати. От і все!

А будь-які багатокутники, як ви знаєте, можна намалювати за допомогою відрізків. Завдання вирішена.

розрахунки

Припустимо, є певний об'єкт, положенняякого по осі X характеризується двома числами: починається він в точці з координатою (-3) і закінчується в (+2). Якщо ми хочемо дізнатися довжину цього предмета, то повинні відняти від більшого числа менше. Зверніть увагу, що негативне число поглинає знак віднімання, тому що «мінус на мінус дає плюс». Отже, ми складаємо (2 + 3) і отримуємо 5. Це і є необхідний результат.

Інший приклад: нам дана кінцева точка і довжина об'єкта, але не дана початкова (і потрібно її знайти). Нехай положення відомої точки буде (6), а розмір досліджуваного предмета - (4). Віднімаючи довжину з кінцевої координати, ми отримаємо відповідь. Разом: (6 - 4) = 2.

Негативні числа

Нерідко потрібно на практиці працювати знегативними значеннями. У цьому випадку ми будемо йти по осі координат вліво. Наприклад, об'єкт висотою 3 сантиметри плаває у воді. На третину він занурений в рідину, на дві третини знаходиться на повітрі. Тоді, вибравши в якості осі поверхню води, ми за допомогою найпростіших арифметичних обчислень отримуємо два числа: верхня точка об'єкта має координату (+2), а нижня - (-1) сантиметр.

Неважко помітити, що у випадку з площиною унас утворюється чотири чверті координатної прямої. Кожна з них має свій номер. У першій (верхній правій) частині будуть розташовуватися точки, що мають дві позитивні координати, в другій - зліва зверху - значення по осі «ікс» будуть негативні, а по «ігрек» - позитивні. Третя і четверта відраховуються далі проти годинникової стрілки.

важлива властивість

Ви знаєте, що пряму можна уявити якбезліч точок. Ми можемо переглянути як завгодно уважно будь-яку кількість значень в кожну сторону осі, але не зустрінемо повторюваних. Це здається наївним і зрозумілим, але виникає то твердження з важливого факту: кожному числу відповідає одна і тільки одна точка на координатній прямій.

висновок

Пам'ятайте, що будь-які осі, фігури і по можливостіграфіки необхідно будувати по лінійці. Одиниці вимірювань були придумані людиною не випадково - допустивши похибка при кресленні, ви ризикуєте побачити вже не те зображення, яке повинно було статися.

Будьте уважні і обережні в побудовіграфіків і обчисленнях. Як і будь-яка наука, яка вивчалася в школі, математика любить точність. Прикладіть трохи старання, і гарні оцінки не змусять себе довго чекати.